Линеаризация характеристик датчиков

Линеаризация характеристик датчиков — нелинейное преобразование выходной величины датчика или величины (аналоговой или цифровой), ей пропорциональной, посредством которого достигается линейная зависимость между измеряемой и представляющей ее величинами.

Пользуясь линеаризацией, можно добиться линейности шкалы вторичного прибора, к которому подключен датчик с нелинейной характеристикой (например, термопара, термосопротивление, газоанализатор, расходомер и др.). Линеаризация характеристик датчиков дает возможность получить требуемую точность измерения вторичными приборами с цифровым выходом. Она необходима в ряде случаев при подключении датчиков к записывающим приборам или при выполнении над измеряемой величиной математических операций (например, интегрирования).

По отношению к характеристике датчика линеаризация выступает как обратное функциональное преобразование. Если характеристику датчика представить как y=F (а + bх), где х — измеряемая величина, а и b — постоянные, то характеристика линеаризатора, включаемого последовательно с датчиком (рис. 1), должна иметь вид: z=kF (у), где F — функция, обратная F.

В результате на выходе линеаризатора будет получено z = kF(F(a+bx)) = a’+b’x, т. е. линейная функция измеряемой величины.

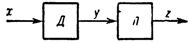
Рис. 1. Обобщенная блок-схема линеаризации: Д— датчик, Л — линеаризатор.

В дальнейшем путем масштабирования зависимость z приводится к виду z’ = mx, где m — соответствующий масштабный коэффициент. Если линеаризация производится компенсационным способом, т. е. на основе следящей системы типа рис. 2, то характеристика линеаризующего преобразователя функционального должна быть подобна характеристике датчика z = cF (a+bx), т. к. линеаризованное значение измеряемой величины снимается со входа функционального преобразователя-линеаризатора, а выход его сравнивается с выходной величиной датчика.

Особенностью линеаризаторов как функциональных преобразователей является сравнительно узкий класс воспроизводимых ими зависимостей, ограничивающийся монотонными функциями, что определяется видом характеристик датчиков.

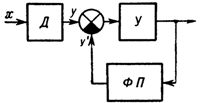
Рис. 2. Блок-схема линеаризации на основе следящей системы: Д — датчик, У — усилитель (преобразователь), ФП — функциональный преобразователь.

Линеаризаторы можно классифицировать по следующим признакам:

1. По способу задания функции: пространственному в виде шаблонов, матриц и т. п., в виде комбинации нелинейных элементов , в виде алгоритма цифрового вычислит, устройства.

2. По степени гибкости схемы: универсальные (т. е. перенастраиваемые) и специализированные.

3. По характеру структурной схемы: разомкнутого (рис. 1) и компенсационного (рис. 2) типов.

4. По форме входных и выходных величин: аналоговые, цифровые, смешанного характера (аналого-цифровые и цифро-аналоговые).

5. По типу применяемых в схеме элементов: механические, электромеханические, магнитные, электронные и др.

К числу линеаризаторов с пространственным заданием функции прежде всего относятся механизмы на кулачках, лекалах и нелинейных потенциометрах. Они используются в тех случаях, когда измеряемая величина на какой-либо ступени преобразования представлена в виде механического перемещения (кулачки — для линеаризации характеристик манометрических и трансформаторных датчиков, лекала — в самопишущих приборах, нелинейные потенциометры — в потеициометрических и мостовых схемах).

Нелинейность характеристик потенциометров достигается намоткой на профилированных каркасах и секционированием по методу кусочно-линейной аппроксимации путем шунтирования секций соответствующими сопротивлениями.

В линеаризаторе, основанном на электромеханической следящей системе потеициометрического типа с использованием нелинейного потенциометра (рис. 3), линеаризованная величина выступает в виде угла поворота или механического перемещения. Эти линеаризаторы просты, универсальны и широко распространены в системах централизованного контроля.

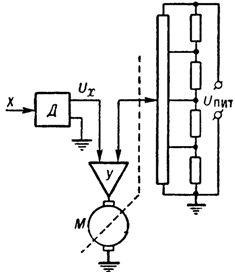
Рис. 3. Линеарнзатор электромеханической следящей системе потенциометрического типа: Д — датчик с выходом в виде пост, напряжения, У — усилитель, М — электродвигатель.

Нелинейности характеристик отдельных элементов (электронных, магнитных, тепловых и др.) используются в параметрических функциональных преобразователях. Однако между отрабатываемыми ими функциональными зависимостями и характеристиками датчиков обычно не удается добиться полного соответствия.

Алгоритмический способ задания функции применяется в цифровых функциональных преобразователях. Их достоинства — высокая точность и стабильность характеристик. В них используются математические свойства отдельных функциональных зависимостей или принцип кусочно-линейной аппроксимации. Например, парабола отрабатывается на основании и свойства квадратов целых чисел.

На методе кусочно-линейной аппроксимации основан, например, цифровой линеаризатор, работающий на принципе заполнения отрезков аппроксимации импульсами различных частот следования. Частоты заполнения изменяются скачками в граничных точках отрезков аппроксимации по программе, закладываемой в устройство в соответствии с видом нелинейности. Линеаризуемая величина преобразуется при этом в унитарный код.

Кусочно-линейная аппроксимация нелинейности может также осуществляться цифровым линейным интерполятором. При этом частоты заполнения интервалов интерполяции остаются постоянными лишь в среднем.

Преимущества цифровых линеаризаторов, основанных на методе кусочно-линейной аппроксимации: легкость перенастройки набранной нелинейности и быстрота переключений с одной нелинейности на другую, что особенно важно в быстродействующих системах централизованного контроля.

В сложных управляющих системах, содержащих универсальные вычислит, машины, линеаризация может выполняться непосредственно этими машинами, в которые функция закладывается в виде соответствующей подпрограммы.

10.12.2016 Информация Нет комментариев