В электрических цепях довольно часто встречается
смешанное соединение,
представляющее собой комбинацию последовательного и параллельного
соединений. Если взять, например, три прибора, то возможны два варианта
смешанного соединения. В одном случае соединяются два прибора
параллельно, а к ним последовательно подключается третий. Такая
цепь имеет два последовательно включенных участка, один из которых
представляет собой параллельное соединение. По другой схеме соединены
последовательно …

В электрических цепях довольно часто встречается смешанное соединение, представляющее собой комбинацию последовательного и параллельного соединений. Если взять, например, три прибора, то возможны два варианта смешанного соединения. В одном случае соединяются два прибора параллельно, а к ним последовательно подключается третий (рис. 1, а).

Такая цепь имеет два последовательно включенных участка, один из которых представляет собой параллельное соединение. По другой схеме соединены последовательно два прибора, а параллельно к ним подключен третий (рис. 1, б). Эту цепь следует рассматривать как параллельное соединение, в котором одна ветвь сама является последовательным соединением.

При большем количестве приборов могут быть различные, более сложные схемы смешанного соединения. Иногда встречаются более сложные цепи, содержащие несколько источников ЭДС.

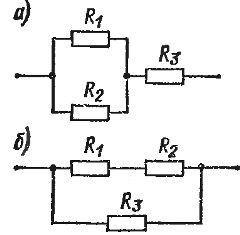
Рис. 1. Смешанное соединение резисторов

Для расчета сложных цепей существуют различные методы. Наиболее общим из них является применение второго закона Кирхгофа. В самом общем виде этот закон гласит, что во всяком замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений.

Необходимо брать алгебраическую сумму потому, что ЭДС, действующие навстречу друг другу, или падения напряжения, созданные противоположно направленными токами, имеют разные знаки.

При расчете сложной цепи в большинстве случаев бывают известны сопротивления отдельных участков цепи и ЭДС, включенных источников. Чтобы найти токи, следует в соответствии со вторым законом Кирхгофа составить для замкнутых контуров уравнения, в которых токи являются неизвестными величинами. К этим уравнениям надо добавить уравнения для точек разветвления, составленные по первому закону Кирхгофа. Решая эту систему уравнений, определим токи. Конечно, для более сложных цепей этот метод получается довольно громоздким, так как приходится решать систему уравнений с большим числом неизвестных.

Применение второго закона Кирхгофа можно показать на следующих простейших примерах.

Пример 1. Дана электрическая цепь (рис. 2). ЭДС источников равны Е1= 10 В и Е2 = 4 В, а внутренние сопротивления г1 = 2 Ом и r2 = 1 Ом соответственно. ЭДС источников действуют навстречу. Нагрузочное сопротивление R = 12 Ом. Найти ток I в цепи.

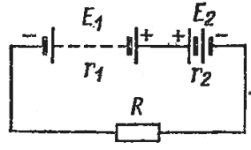
Рис. 2. Электрическая цепь с двумя источниками, включенными навстречу друг другу

Решение. Так как в данном случае имеется лишь один замкнутый контур, то составляем одно единственное уравнение: E1 — E2 = IR + Ir1 + Ir2.

В левой его части имеем алгебраическую сумму ЭДС, а в правой части — сумму падений напряжений, создаваемых током I на всех последовательно включенных участках R, r1 и r2.

Иначе уравнение можно написать в таком виде:

Е1 — Е2 = I (R = r1 + r2)

или I = (Е1 — Е2) /(R + r1 + r2)

Подставив числовые значения, получим: I = (10 — 4)/(12 + 2 + 1) = 6/15 = 0,4 А.

Эту задачу, конечно, можно было решить на основании закона Ома для всей цепи, имея в виду, что при включении двух источников ЭДС навстречу друг другу, действующая ЭДС равна разности E1— Е2, в общее сопротивление цепи является суммой сопротивлений всех включенных приборов.

Пример 2. Более сложная схема представлена на рис. 3.

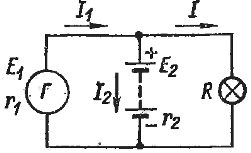
Рис. 3. Параллельная работа источников, имеющих разные ЭДС

На первый взгляд она кажется довольно простой. Два источника (для примера взят генератор постоянного тока и аккумуляторная батарея) соединены параллельно и к ним подключена лампочка. ЭДС и внутренние сопротивления источников соответственно равны: Е1 = 12 В, Е2 = 9 В, r1 = 0,3 Ом, r2 = 1 Ом. Сопротивление лампочки R = 3 Ом Необходимо найти токи I1, I2, I и напряжение U на зажимах источников.

Поскольку ЭДС Е1 больше, чем Е2, то в данном случае генератор Е1, очевидно, заряжает аккумулятор и одновременно питает лампочку. Составим уравнения по второму закону Кирхгофа.

Для контура, состоящего из обоих источников, Е1 — E2 = I1rl = I2r2.

Уравнение для контура, состоящего из генератора Е1 и лампочки, имеет вид Е1 = I1rl + I2r2.

И, наконец, в контуре, в который входит аккумулятор и лампочка, токи направлены навстречу друг другу и поэтому для него Е2 = IR — I2r2. Эти три уравнения недостаточны для определения токов, так как только два из них являются независимыми, а третье может быть получено из двух других. Поэтому надо взять любые два из этих уравнений и в качестве третьего написать уравнение по первому закону Кирхгофа: I1 = I2 + I.

Подставив в уравнения числовые значения величин и решив их совместно, получим: I1= 5 А, I2 = 1,5 А, I = 3,5 A, U = 10,5 В.

Напряжение на зажимах генератора на 1,5 В меньше его ЭДС, так как ток, равный 5 А, создает потери напряжения, равные 1,5 В, на внутреннем сопротивлении г1 = 0,3 Ом. Зато напряжение на зажимах аккумуляторной батареи больше ее ЭДС на 1,5 В, потому что батарея заряжается током, равным 1,5 А. Этот ток создает на внутреннем сопротивлении батареи (г2 = 1 Ом) падение напряжения, равное 1,5 В, оно и прибавляется к ЭДС.

Не следует думать, что напряжение U всегда будет средним арифметическим E1 и Е2, как это оказалось в данном частном случае. Можно только утверждать, что в любом случае U должно находиться между Е1 и Е2.

10.12.2016 Без рубрики Нет комментариев