 Помимо
Помимо
простых, т. е. синусоидальных переменных токов, часто встречаются
сложные токи, у которых график изменения тока во времени является не
синусоидой, а более сложной кривой. Иначе говоря, у подобных токов закон
изменения тока во времени является более сложным, нежели у простого
синусоидального тока. Изучение
этих токов основано на том, что всякий сложный несинусоидальный ток
можно считать состоящим из нескольких простых синусоидальных токов, у которых амплитуды различны, а частоты в целое число раз больше частоты данного сложного тока …
 Помимо простых, т. е. синусоидальных переменных токов, часто встречаются сложные токи, у которых график изменения тока во времени является не синусоидой, а более сложной кривой. Иначе говоря, у подобных токов закон изменения тока во времени является более сложным, нежели у простого синусоидального тока. Пример такого тока показан на рис. 1.
Помимо простых, т. е. синусоидальных переменных токов, часто встречаются сложные токи, у которых график изменения тока во времени является не синусоидой, а более сложной кривой. Иначе говоря, у подобных токов закон изменения тока во времени является более сложным, нежели у простого синусоидального тока. Пример такого тока показан на рис. 1.
Изучение этих токов основано на том, что всякий сложный несинусоидальный ток можно считать состоящим из нескольких простых синусоидальных токов, у которых амплитуды различны, а частоты в целое число раз больше частоты данного сложного тока. Подобное разложение сложного тока на ряд простых токов важно потому, что во многих случаях изучение сложного тока удается свести к рассмотрению простых токов, для которых в электротехнике выведены все основные законы.
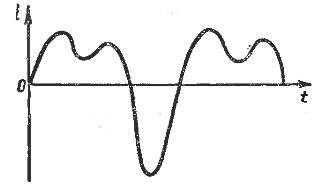
Рис. 1. Сложный несинусоидальный ток
Простые синусоидальные токи, входящие в состав сложного тока, называются гармониками и нумеруются в порядке возрастания их частоты. Например, если сложный ток имеет частоту 50 Гц, то его первая гармоника, называемая иначе основным колебанием, представляет собой синусоидальный ток с частотой 50 Гц, вторая гармоника является синусоидальным током с частотой 100 Гц, третья гармоника имеет частоту 150 Гц и т. д.
Номер гармоники показывает, во сколько раз ее частота больше частоты данного сложного тока. С повышением номера гармоник амплитуды их обычно уменьшаются, но бывают исключения из этого правила. Иногда некоторые гармоники вообще отсутствуют, т. е. амплитуды их равны нулю. Только первая гармоника имеется всегда.
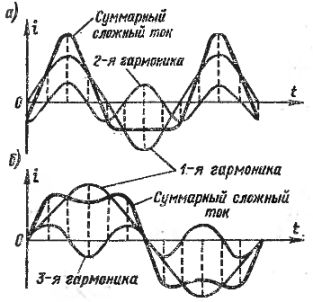
Рис. 2. Сложный переменный ток и его гармоники
В качестве примера на рис. 2, а изображен график сложного тока, состоящего из первой и второй гармоник, и графики этих гармоник, а на рис. 2, б то же показано для тока, состоящего из первой и третьей гармоник. На этих графиках сложение гармоник и получение суммарного тока сложной формы осуществляется сложением вертикальных отрезков, изображающих токи в разные моменты времени, с учетом их знаков (плюс и минус).
Иногда сложный ток, кроме гармоник, имеет в своем составе еще и постоянный ток, т. е. постоянную составляющую. Так как частота постоянного тока равна нулю, то постоянную составляющую можно назвать нулевой гармоникой.
Найти гармоники сложного тока довольно трудно. Этому посвящен специальный раздел математики, называемый гармоническим анализом. Однако по некоторым признакам можно судить о наличии тех или иных гармоник. Например, если положительная и отрицательная полуволны сложного тока одинаковы по форме и максимальному значению, то в таком токе содержатся только одни нечетные гармоники.
Пример подобного тока дан на рис. 2, б. Если же положительная и отрицательная полуволны отличаются друг от друга по форме и максимальному значению (рис. 2, а), то это служит признаком наличия четных гармоник (при этом могут быть и нечетные гармоники).
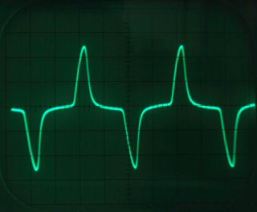
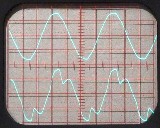
Рис. 3. Сложный переменный ток на экране осциллографа
Переменные напряжения и ЭДС сложной формы подобно сложным токам могут быть представлены в виде суммы простых синусоидальных составляющих.
По поводу физического смысла разложения сложных токов на гармоники можно повторить то, что говорилось о пульсирующем токе, который также следует отнести к сложным токам.
В электрических цепях, состоящих из линейных приборов, действие сложного тока всегда можно рассматривать и рассчитывать как суммарное действие составляющих его токов. Однако при наличии нелинейных приборов этот метод имеет более ограниченное применение, так как в решении ряда вопросов он может дать существенные ошибки.
Смотрите также по этой теме: Расчет цепей несинусоидального тока