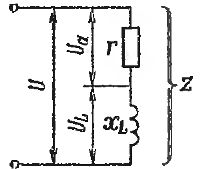
При последовательном соединении приборов с активным и индуктивным сопротивлениями (рис. 1) полное сопротивление цепи нельзя находить арифметическим суммированием. Если обозначить полное сопротивление через z, то для его определения служит формула:

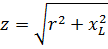
Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Так, например, если r = 30 Ом и XL = 40 Ом, то

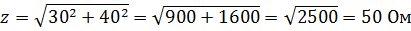
т. е. z получилось меньше, чем r + XL = 30 + 40 = 70 Ом.

Для упрощения расчетов полезно знать, что если одно из сопротивлений (r или xL) превосходит другое в 10 или более раз, то можно пренебречь меньшим сопротивлением и считать, что z равно большему сопротивлению. Ошибка весьма невелика.

Например, если r = 1 Ом и xL = 10 Ом, то

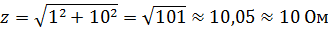
Ошибка лишь 0,5 % вполне допустима, так как сами сопротивления r и х бывают известны с меньшей точностью.

Итак, если

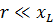
То

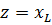
а если

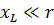
То

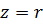
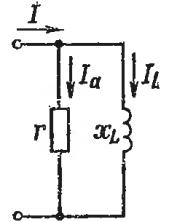
При параллельном соединении ветвей, имеющих активные и реактивные сопротивления (рис. 2), расчет полного сопротивления удобнее делать с помощью активной проводимости

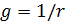
и реактивной проводимости

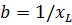
Полная проводимость цепи у равна геометрической сумме, активной и реактивной проводимостей:

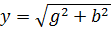
А полное сопротивление цепи является величиной, обратной у,

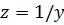
Если выразить проводимость через сопротивления, то нетрудно получить следующую формулу:

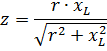
Эта формула напоминает известную формулу

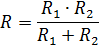
но только в знаменателе стоит не арифметическая, а геометрическая сумма сопротивлений ветвей.

Пример. Найти полное сопротивление, если параллельно соединены приборы, имеющие r = 30 Он и xL = 40 Ом.

Решение.

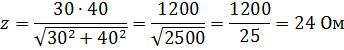
При расчете z для параллельного соединения можно для упрощения пренебречь большим сопротивлением, если оно превосходит меньшее в 10 и более раз. Ошибка не будет превышать 0,5 %

Рис. 1. Последовательное соединение участков цепи с активным и индуктивным сопротивлением

Рис. 2. Параллельное соединение участков цепи с активным и индуктивным сопротивлением

Следовательно, если

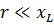
То

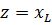
а если

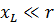
То

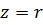
Принцип геометрического сложения применяется для цепей переменного тока также в случаях, когда надо складывать активные и реактивные напряжения или токи. Для последовательной цепи по рис. 1 складываются напряжения:

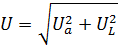
При параллельном соединении (рис. 2) складываются токи:

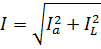
Если же последовательно или параллельно соединены приборы, имеющие только одни активные или только одни индуктивные сопротивления, то сложение сопротивлений или проводимостей и соответствующих напряжений или токов, а также активных или реактивных мощностей производится арифметически.

При любой цепи переменного тока закон Ома можно писать в следующем виде:

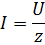
где z — полное сопротивление, вычисляемое для каждого случая соединения так, как это было показано выше.

Коэффициент мощности cos для любой цепи равен отношению активной мощности Р к полной S. При последовательном соединении это отношение можно заменить отношением напряжений или сопротивлений:

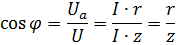
При параллельном соединении получим:

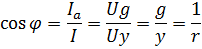
Навигация по записям