Символический метод операций с векторными величинами
основывается на весьма простой идее: каждый вектор раскладывают на две
составляющие: одну — горизонтальную, идущую по оси абсцисс, а вторую —
вертикальную, идущую по оси ординат. В этом случае все горизонтальные
составляющие идут по одной прямой, и их можно складывать с помощью
простого алгебраического сложения, аналогичным образом складывают и
вертикальные составляющие. При таком подходе в общем случае получаются …

Символический метод операций с векторными величинами основывается на весьма простой идее: каждый вектор раскладывают на две составляющие: одну — горизонтальную, идущую по оси абсцисс, а вторую — вертикальную, идущую по оси ординат. В этом случае все горизонтальные составляющие идут по одной прямой, и их можно складывать с помощью простого алгебраического сложения, аналогичным образом складывают и вертикальные составляющие.

При таком подходе в общем случае получаются две результирующие составляющие — горизонтальная и вертикальная, которые всегда находятся друг к другу под одним и тем же углом, равным 90°.

По этим составляющим можно найти их равнодействующую, т. е. произвести их геометрическое сложение. Составляющие под прямым углом представляют катеты прямоугольного треугольника, а их геометрическая сумма — гипотенузу.

Можно также сказать, что геометрическая сумма численно равна диагонали параллелограмма, построенного на составляющих, как на его сторонах. Если горизонтальную составляющую обозначить АГ а вертикальную — АВ, то геометрическая сумма (1)

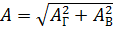
Находить геометрическую сумму прямоугольных треугольников гораздо легче, чем косоугольных. Легко видеть, что (2)

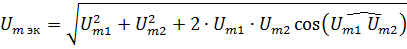
превращается в (1) если угол между составляющими составляет 90°. Поскольку cos 90 = 0, последний член в подкоренном выражении (2) исчезает, вследствие чего выражение резко упрощается. Обратим внимание на то, что перед словом «сумма» обязательно следует добавлять одно из трех слов: «арифметическая», «алгебраическая», «геометрическая».

Рис.1.

Слово «сумма» без указания, какая именно, приводит к неопределенности, а в ряде случаев и к грубым ошибкам.

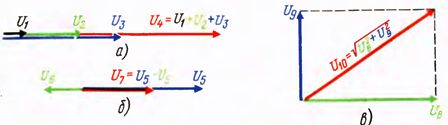
Напомним, что результирующий вектор равен арифметической сумме векторов в том случае, когда все векторы идут по одной прямой (или параллельно друг другу) в одинаковом направлении. При этом все векторы имеют знак плюс (рис. 1, а).

Если векторы идут по одной прямой, но направлены в противоположные стороны, то их равнодействующая равна алгебраической сумме векторов, в этом случае одни члены имеют знак плюс, а другие минус.

Например, в схеме рис. 1, б U6 = U4 — U5. Можно также сказать, что арифметическую сумму используют в тех случаях, когда угол между векторами равен нулю, алгебраическую, когда углы составляют 0 и 180°. Во всех остальных случаях сложение производят векторно, т. е. определяют геометрическую сумму (рис. 1, в).

Пример. Определить параметры эквивалентной синусоиды для цепи рис. 2, а символическим методом.

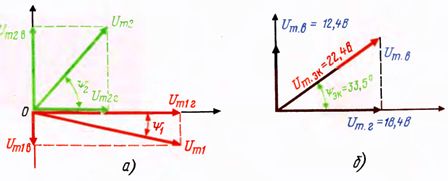
Решение. Нарисуем векторы Um1 Um2 и разложим их на составляющие. Из чертежа видно, что каждая горизонтальная составляющая представляет значение вектора, умноженное на косинус фазного угла, а вертикальная — значение вектора, умноженное на синус фазного угла. В данном случае

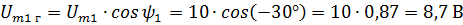
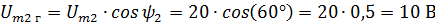
Рис.2.

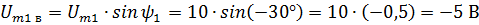
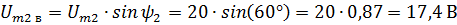
Очевидно, что общие горизонтальные и вертикальная составляющие равны алгебраическим суммам соответствующих составляющих. В данном случае

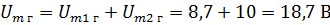
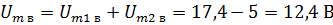
Получившиеся составляющие покажем на рис. 2, б. Определим значение Um для этого вычислим геометрическую сумму обеих составляющих:

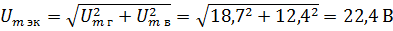
Определим эквивалентный фазный угол эк. Из рис. 2,б видно, что отношение вертикальной составляющей к горизонтальной представляет тангенс эквивалентного фазного угла.