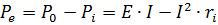Если в рассматриваемой
Если в рассматриваемой
ветви вместо резистора включен какой-либо другой преобразователь
электромагнитной энергии в механическую или химическую, или другую форму
энергии (электрический мдвигатель, заряжающийся аккумулятор и т.п.), работу,
проделанную током за время t, можно подсчитать в том случае, если
известно напряжение на преобразователе.
во всей внешней цепи, и мощность, отдаваемая генератором, одна и та же
величина. Мощность, развиваемая генератором, всегда больше …
Согласно закону Джоуля—Ленца работа, совершаемая постоянным током в сопротивлении,
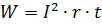
Если в рассматриваемой ветви вместо резистора включен какой-либо другой преобразователь электромагнитной энергии в механическую или химическую, или другую форму энергии (электрический двигатель, заряжающийся аккумулятор и т.п.), работу, проделанную током за время t, можно подсчитать в том случае, если известно напряжение на преобразователе.
В этом случае формула Джоуля—Ленца приобретает другой вид:
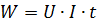
При постоянном токе мощность, поступающая в участок цепи с сопротивлением r, определяется выражением:
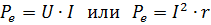
где I, U и r сохраняют тот же смысл, что и в формуле Джоуля—Ленца.
Мощность, расходуемая во всей внешней цепи, и мощность, отдаваемая генератором, одна и та же величина. Мощность, развиваемая генератором, всегда больше той, которую генератор отдает во внешнюю цепь, так как часть мощности расходуется на покрытие потерь внутри самого генератора.
Выражение баланса мощностей для одиночного замкнутого контура, содержащего генератор с э.д.с. Е и внутренним сопротивлением ri и резистор с сопротивлением r, можно получить из уравнения Кирхгофа.
Для этого контура
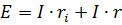
Если обе части этого равенства умножить на ток в цепи, то полученное уравнение и будет представлять собой баланс мощностей в данном контуре
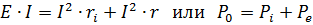
Мощность, развиваемая генератором, равна сумме мощностей теряемой внутри генератора и отдаваемой во внешнюю цепь. Р0 = EI — мощность, развиваемая генератором, Pe = UI=I2r — мощность, отдаваемая генератором во внешнюю цепь, и Pi — I2ri — мощность, теряемая внутри самого генератора.
При выборе одинаковых положительных направлений тока через двухполюсник I и напряжения на двухполюснике U мощность, потребляемая двухполюсником, т. е. Произведение UI, должно быть положительно. Если же при этом окажется, что произведение UI отрицательно, это будет означать, что двухполюсник не потребляет электромагнитную энергию, а наоборот является генератором электромагнитной энергии и отдает эту энергию в электрическую цепь.
Если в электрической цепи ряд двухполюсников отдает электромагнитную энергию в цепь, то остальные эту энергию поглощают. В цепи при постоянном токе не может происходить накопления электромагнитной энергии. Поэтому сумма мощностей, расходуемых в пассивных двухполюсниках и мощностей, теряемых внутри генераторов, должна быть равна алгебраической сумме мощностей, развиваемых всеми генераторами, т. е. сумме произведений ЕкIк всех генераторов, действующих в цепи:
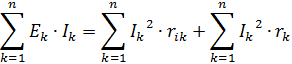
где n — число ветвей в цепи.
Уравнение баланса, полученное для простой цепи, содержащей один генератор, можно переписать, выразив мощность, расходуемую во внешней цепи, через мощность, развиваемую генератором, и мощность, теряемую внутри генератора: