Графическое изображение синусоидальных величин

В
любой линейной цепи вне зависимости от вида элементов, входящих в цепь,
гармоническое напряжение вызывает гармонический ток и, наоборот,
гармонический ток порождает напряжения на зажимах этих элементов также
гармонической формы. Обратим внимание, что индуктивности катушек и
емкости конденсаторов предполагаются также величинами линейными. В
более общем случае можно сказать, что в линейных цепях при
гармонических воздействиях все отклики имеют также гармоническую форму …

В любой линейной цепи вне зависимости от вида элементов, входящих в цепь, гармоническое напряжение вызывает гармонический ток и, наоборот, гармонический ток порождает напряжения на зажимах этих элементов также гармонической формы. Обратим внимание, что индуктивности катушек и емкости конденсаторов предполагаются также величинами линейными.

В более общем случае можно сказать, что в линейных цепях при гармонических воздействиях все отклики имеют также гармоническую форму. Следовательно, в любой линейной цепи все мгновенные напряжения и токи имеют одну и ту же гармоническую форму. Если цепь содержит хотя бы несколько элементов, то синусоидальных кривых становится достаточно много, эти временные диаграммы накладываются друг на друга, чтение их сильно затрудняется, изучение становится предельно неудобным.

По указанным причинам изучение процессов, происходящих в цепях при гармонических воздействиях, производят не на кривых синусоидальной формы, а с помощью векторов, длины которых берутся пропорциональными максимальным значениям кривых, а углы, под которыми откладываются векторы, равными углам между началами двух кривых или началом кривой и началом координат. Таким образом, вместо временных диаграмм, занимающих много места, приводят их изображения в виде векторов, т. е. прямых линий со стрелками на концах, причем у векторов напряжения стрелки показывают заштрихованными, а у векторов тока оставляют незаштрихованными.

Совокупность векторов напряжений и токов в цепи называется векторной диаграммой. Правило отсчета углов на векторных диаграммах следующее: если необходимо показать вектор, отстающий от начального положения на некоторый угол, то поворачивают вектор на данный угол по часовой стрелке. Вектор, повернутый против часовой стрелки, означает опережение на указанный угол.

Например, на схеме рис. 1 показаны три временные диаграммы с одинаковыми амплитудами, но различными начальными фазами. Следовательно, длины векторов, соответствующих этим гармоническим напряжениям, должны быть одинаковыми, а углы — разными. Проведем взаимно перпендикулярные координатные оси, за начало отсчета примем горизонтальную ось с положительными значениями, в этом случае вектор первого напряжения должен совпадать с положительной частью горизонтальной оси, вектор второго напряжения — быть повернутым по часовой стрелке на угол 2, а вектор третьего напряжения — против часовой стрелки на угол (рис. 1).

Длины векторов зависят от выбранного масштаба, иногда их проводят произвольной длины с соблюдением пропорций. Поскольку максимальные и действующие значения всех гармонических величин отличаются всегда в одно и то же число раз (в 2= 1,41), то на векторных диаграммах можно откладывать как максимальные, так и действующие значения.

Временная диаграмма показывает значение гармонической функции в любой момент в соответствии с уравнением u = Um sin t. На векторной диаграмме также можно показать значения в каждый момент времени. Для этого необходимо представить вектор вращающимся в направлении против часовой стрелки с угловой скоростью и брать проекцию этого вектора на вертикальную ось. Получившиеся длины проекций будут подчиняться закону u = Um sint и, следовательно, представлять мгновенные значения в том же масштабе. Направление вращения вектора против часовой стрелки считают положительным, а по часовой стрелке — отрицательным.

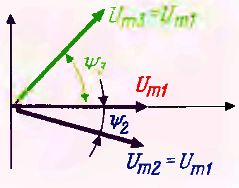
Рис.1

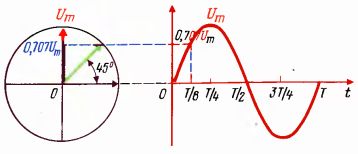
Рис.2

Рис.3

Рассмотрим пример определения мгновенных значений напряжений с помощью векторной диаграммы. В правой части рис. 2 показана диаграмма временная, а в левой части — векторная. Пусть начальный фазный угол равен нулю. В этом случае в момент t = 0 мгновенное значение напряжения равно нулю, а вектор, соответствующий этой временной диаграмме, совпадает с положительным направлением оси абсцисс, проекция этого вектора на вертикальную ось в этот момент также равна нулю, т. е. длина проекции совпадает с мгновенным значением синусоиды.

Через время t = Т/8 фазный угол становится равным 45°, а мгновенное значение Um sin t = Um sin 45° = = 0,707 Um. Но радиус-вектор за это время повернется также на угол 45° и проекция этого вектора станет также 0,707 Um. Через t = Т/4 мгновенное значение кривой достигнет U , но и радиус-вектор поворачивается также на 90°. Проекция на вертикальную ось в этот момент станет равной самому вектору, длина которого пропорциональна максимальному значению. Аналогичным образом можно определить мгновенные значения в любой момент.

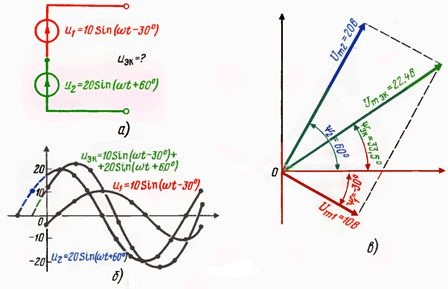
Таким образом, все операции, которые тем или иным образом приходится производить с синусоидальными кривыми, сводятся к операциям, выполняемым не с самими синусоидами, а с их изображениями, т. е. с соответствующими им векторами. Например, имеется цепь рис. 3, а, в которой необходимо определить эквивалентную кривую мгновенных значений напряжения. Чтобы построить суммарную кривую графическим способом, необходимо произвести весьма громоздкую операцию графического сложения двух кривых, выполняемых по точкам (рис. 3, б). Для аналитического сложения двух синусоид необходимо найти максимальное значение эквивалентной синусоиды: