Изучение
переменного тока весьма затруднительно, если изучающий не усвоил
основных сведений из тригонометрии. Поэтому основные положения
тригонометрии, которые могут понадобиться в дальнейшем, мы приводим в начале этой статьи. Известно,
что в геометрии принято, рассматривая прямоугольный треугольник,
называть сторону, лежащую против прямого угла, гипотенузой. Стороны,
примыкающие к прямому углу, называются катетами. Прямой угол имеет 90°.
Таким образом,  гипотенузой является сторона, обозначенная
буквами …

Основные сведения из тригонометрии

Изучение переменного тока весьма затруднительно, если изучающий не усвоил основных сведений из тригонометрии. Поэтому основные положения тригонометрии, которые могут понадобиться в дальнейшем, мы приводим в начале этой статьи.

Известно, что в геометрии принято, рассматривая прямоугольный треугольник, называть сторону, лежащую против прямого угла, гипотенузой. Стороны, примыкающие к прямому углу, называются катетами. Прямой угол имеет 90°. Таким образом, на рис. 1 гипотенузой является сторона, обозначенная буквами Об, катетами же стороны аб и аО.

На рисунке отмечено, что прямой угол имеет 90°, два другие угла треугольника являются острыми и обозначены буквами (альфа) и (бета).

Если измерить в определенном масштабе стороны треугольника и взять отношение величины катета, лежащего против угла , к величине гипотенузы, то такое отношение называют синусом угла . Синус угла принято обозначать так: sin . Следовательно, в прямоугольном треугольнике, который мы рассматриваем, синус угла равен:

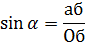
Если составить отношение, взяв величину катета аО, примыкающего к острому углу , к гипотенузе, то это отношение называют косинусом угла Косинус угла принято обозначать следующим образом: сos . Таким образом, косинус угла а равен:

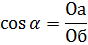
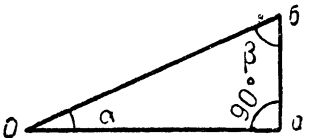
Рис. 1. Прямоугольный треугольник.

Зная синус и косинус угла , можно определить величины катетов. Если умножить величину гипотенузы Об на sin , то получим катет аб. Умножив гипотенузу на сos , получим катет Оа.

Предположим, что угол альфа не остается постоянным, а постепенно изменяется, увеличиваясь. Когда угол равен нулю, синус его также равен нулю, так как нулю район противолежащий углу катет.

По мере того, как угол а будет возрастать, начнет увеличиваться и его синус. Наибольшее значение синуса получится, когда угол альфа станет прямым, то есть будет равен 90°. При этом синус равен единице. Таким образом, синус угла может иметь наименьшее значение—0 и наибольшее—1. Для всех промежуточных значений угла синус является правильной дробью.

Косинус угла будет наибольшим, когда угол равен нулю. При этом косинус равен единице, так как катет, прилежащий к углу, и гипотенуза в этом случае будут совпадать друг с другом, и отрезки, изображающие их, равны между собой. Когда угол равен 90°, косинус его равен нулю.

Графические способы изображения переменного тока

Синусоидальный переменный ток или э.д.с, изменяющиеся во времени, можно изобразить в виде синусоиды. Такой способ изображения часто применяется в электротехнике. Наряду с изображением переменного тока в виде синусоиды широко применяется также изображение такого тока в виде векторов.

Вектором называется величина, имеющая определенное значение и направление. Такую величину представляют в виде отрезка прямой линии со стрелкой на конце. Стрелка должна указывать направление вектора, а отрезок, измеренный в определенном масштабе, дает величину вектора.

Все фазы изменения переменного синусоидального тока за один период можно изобразить при помощи векторов, действуя следующим образом. Предположим, что начало вектора находится в центре окружности, а конец его лежит в самой окружности. Этот вектор, вращаясь по направлению против часовой стрелки, совершает полный оборот за время, соответствующее одному периоду изменения тока.

Проведем из точки, определяющей начало вектора, то есть из центра окружности О, две линии: одну горизонтальную, а другую вертикальную, как это изображено на рис 2.

Если для каждого положения вращающегося вектора из его конца, обозначенного буквою А, опускать перпендикуляры на вертикальную линию, то отрезки этой линии от точки О до основания перпендикуляра а будут давать нам мгновенные значения синусоидального переменного тока, а сам вектор OA в определенном масштабе изображает амплитуду этого тока, то есть его наибольшее значение. Отрезки Оа на вертикальной оси называются проекциями вектора OA на ось у.

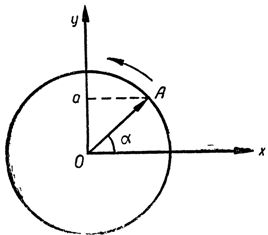
Рис. 2. Изображение изменений синусоидального тока с помощью вектора.

В справедливости изложенного выше не трудно убедиться, выполнив следующее построение. Рядом с окружностью на рисунке можно получить синусоиду,

10.12.2016 Без рубрики Нет комментариев